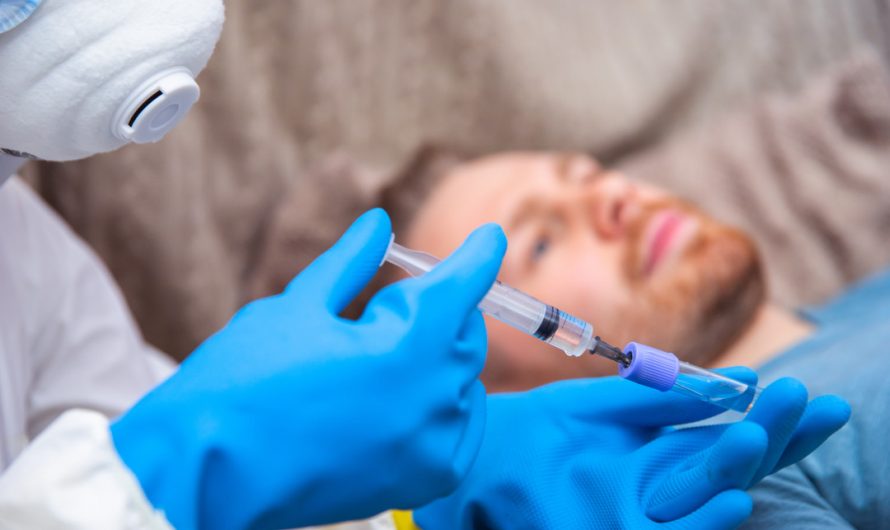
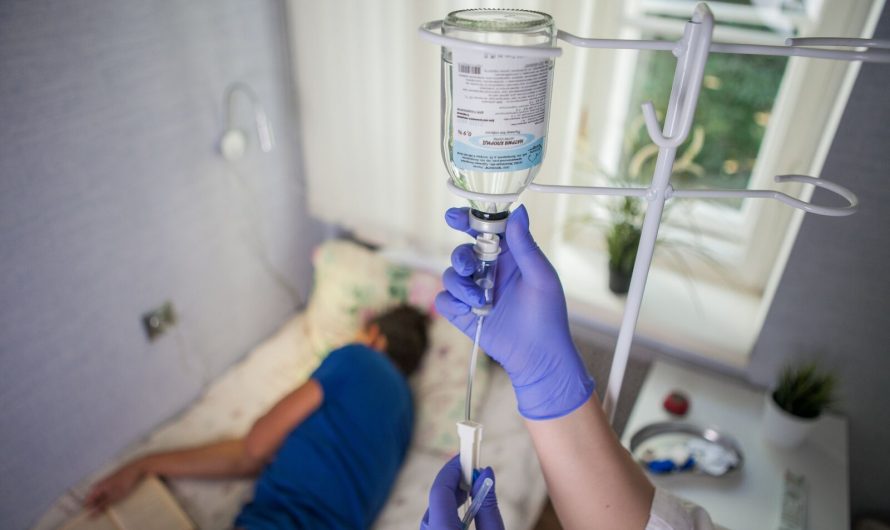
Снятие ломки в Перми: эффективные методы и поддержка
Ломка или абстинентный синдром – тяжелое состояние, которое возникает у людей, страдающих зависимостью от алкоголя, наркотиков или других психоактивных веществ, при резком прекращении их употребления. …